微生物组数据分析方法之:组间差异显著性分析
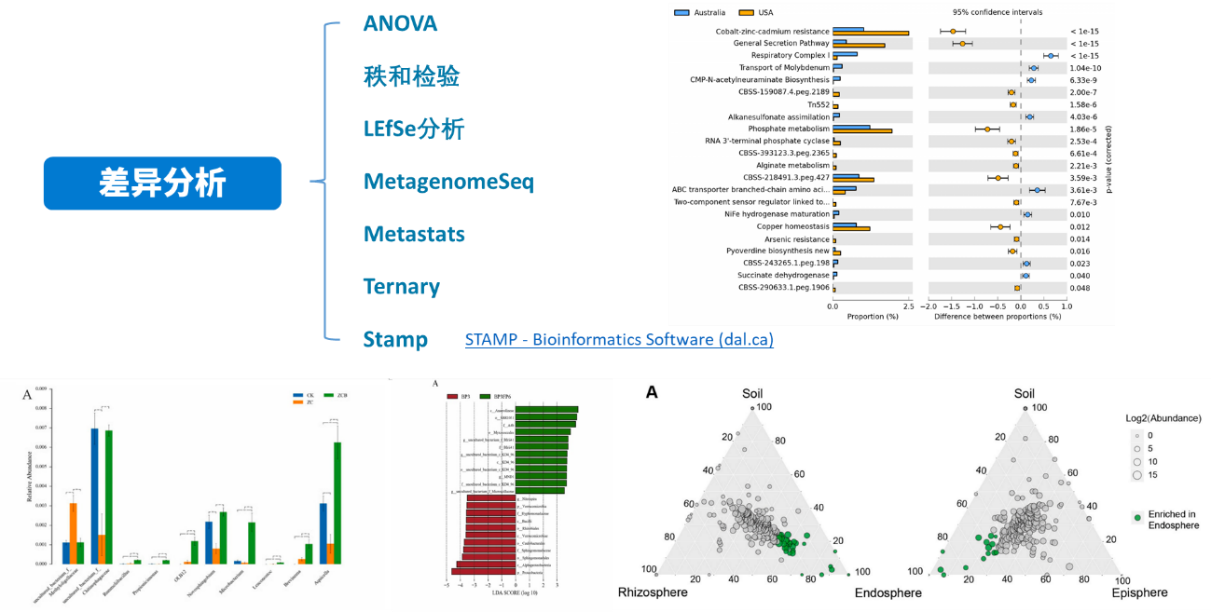
上篇介绍了关于群落结构整体间的差异分析,那么针对不同的处理,不同的环境条件下,究竟是哪些微生物对环境变化更加敏感,在处理组间表现出更显著的差异,而这些微生物又是如何响应环境变化的,是否可以作为指示物种用于后续的实验研究当中,这些就涉及到我们今天要讲的组间差异显著性分析,一起来看下:
ANOVA分析:方差分析(Analysis of Variance,简称ANOVA),又称“变异数分析”或“F检验”, 用于两个及两个以上样本均数差别的显著性检验。它的基本思想是将测量数据的总变异(即总方差)按照变异来源分为处理(组间)效应和误差(组内)效应,通过分析研究不同来源的变异对总变异的贡献大小,从而确定可控因素对研究结果影响力的大小。
(1) 实验条件,即不同的处理造成的差异,称为组间差异,用变量在各组的均值与总均值之偏差平方和的总和表示,记作SSb,组间自由度dfb。
(2) 随机误差,如测量误差造成的差异或个体间的差异,称为组内差异,用变量在各组的均值与该组内变量值之偏差平方和的总和表示,记作SSw,组内自由度dfw。
总偏差平方和 SSt = SSb + SSw。
组内SSw、组间SSb除以各自的自由度(组内dfw =n-m,组间dfb=m-1,其中n为样本总数,m为组数),得到其均方MSw和MSb。
一种情况是处理没有作用,即各组样本均来自同一总体,MSb/MSw≈1。另一种情况是处理确实有作用,组间均方是由于误差与不同处理共同导致的结果,即各样本来自不同总体,那么,MSb>>MSw(远远大于)。MSb/MSw比值构成F分布,用F值与其临界值比较,推断各样本是否来自相同的总体。
常用单因素方差分析(one-way anova)来进行比较,其适用于只有一个因素(自变量)的处理。在观测变量总离差平方和中,如果组间离差平方和所占比例较大,则说明观测变量的变动主要是由控制变量引起的,可以主要由控制变量来解释,控制变量给观测变量带来了显著影响;反之,如果组间离差平方和所占比例小,则说明观测变量的变动不是主要由控制变量引起的,不可以主要由控制变量来解释,控制变量的不同水平没有给观测变量带来显著影响,观测变量值的变动是由随机变量因素引起的。
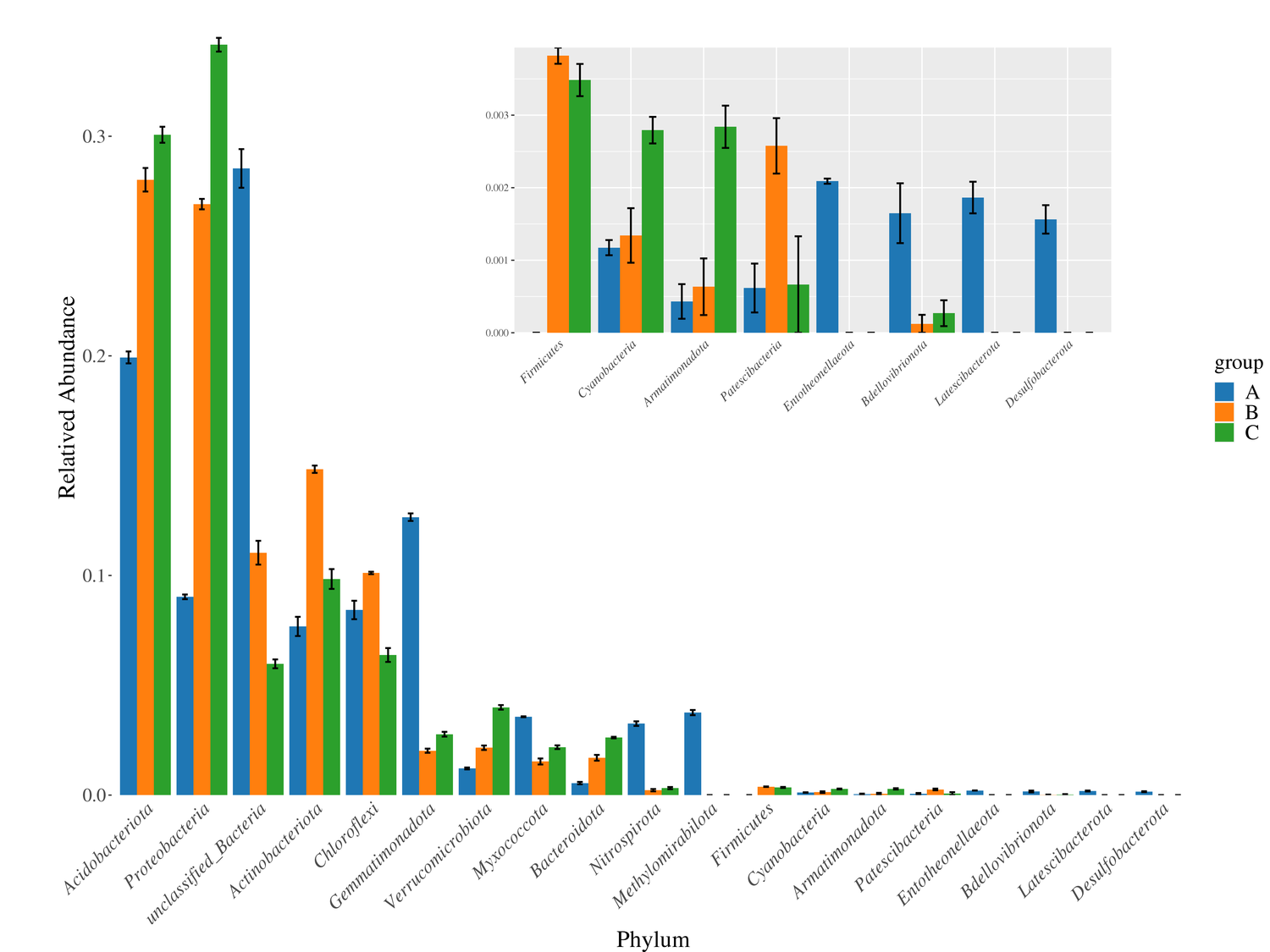 秩和检验:秩和检验是非参数检验的一种方法。其中“秩”又称等级、即上述次序号的和称“秩和”,秩和检验就是用秩和作为统计量进行假设检验的方法。
秩和检验:秩和检验是非参数检验的一种方法。其中“秩”又称等级、即上述次序号的和称“秩和”,秩和检验就是用秩和作为统计量进行假设检验的方法。
当在实践中遇到总体分布类型未知;或者总体分布类型已知但不符合正态分布;或者某些变量可能无法jing q测量;以及方差不齐时,即可采用秩和检验进行分析。
该分析针对不同样本会采用不同分析方法:
1)两组独立样本 — 小样本采用Wilcoxon秩和检验 (Wilcoxon rank-sum test),大样本采用曼-惠特尼 U 检验(Mann–Whitney U test),样本数小于等于20为小样本,样本数大于20为大样本;
2)多组独立样本 — Kruskal-Wallis秩和检验,两两分析可采用Nemenyi法检验,Kruskal-Wallis秩和检验要求每组样本数不得小于5个。
该分析可以对两组或多组样品的物种、基因或者功能进行显著性差异分析,并对 p值进行FDR校正。
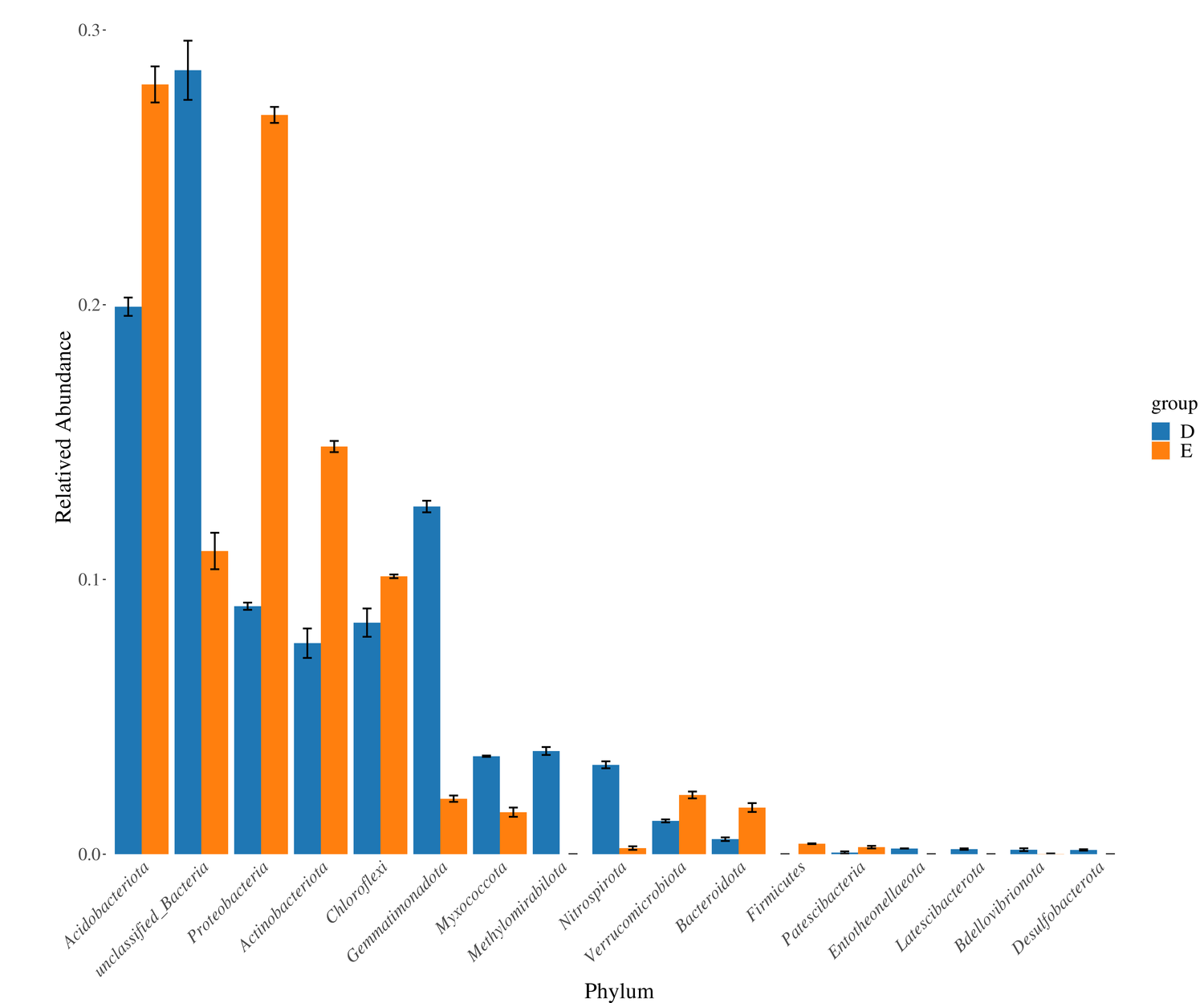 LEfSe分析:LEfSe (Line Discriminant Analysis (LDA) Effect Size)分析是一种将非参数的Kruskal-Wallis以及Wilcoxon秩和检验,与线性判别分析(Linear discriminant analysis,LDA)效应量(Effect size)相结合的分析手段, 能够在不同组间寻找具有统计学差异的Biomarker,其要求组内样本数≥3。
LEfSe分析:LEfSe (Line Discriminant Analysis (LDA) Effect Size)分析是一种将非参数的Kruskal-Wallis以及Wilcoxon秩和检验,与线性判别分析(Linear discriminant analysis,LDA)效应量(Effect size)相结合的分析手段, 能够在不同组间寻找具有统计学差异的Biomarker,其要求组内样本数≥3。
首先使用non-parametric factorial Kruskal-Wallis (KW) sum-rank test(非参数因子克鲁斯卡尔—沃利斯和秩验检)检测具有显著丰度差异特征,并找到与丰度有显著性差异的类群,然后采用线性判别分析(LDA)来估算每个组分(物种)丰度对差异效果影响的大小。
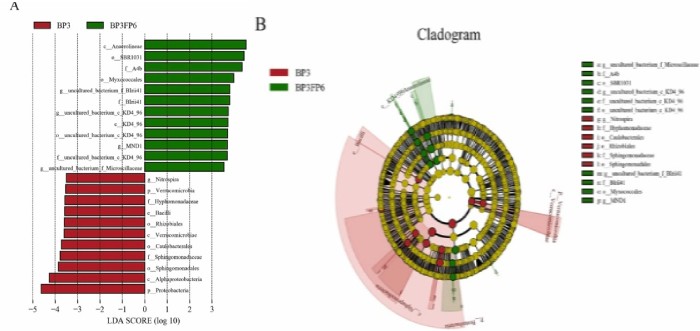
LDA值分布柱状图(上),LEfSe分析进化分枝图(下)
标志物组间丰度柱状图
Metastats分析:用于寻找组间差异物种,从算法原理上来说,Metastats实际上是非参数多重检验和p值校正的整合,由于Metastats采用的非参数t检验,因此只能分析两个分组间差异。对组间的物种丰度数据进行 T 检验得到 p 值,并对 p 值进行校正得到 q 值;最后根据 p 值(或 q 值)筛选出导致两组样品组成差异的物种,进而进行可视化绘图,得到相应的物种差异柱状图,或者箱线图展示。
Metagenomeseq分析:Metagenomseq方法是近几年出现的新的两组间检验的方法,用normalization实现分类注释时的biases处理,同时用零膨胀高斯分布(zero-flated Gaussian distribution)处理了测序深度所带来的影响,在此基础上,利用线性模型找到存在的差异所在。用于研究两组样品间微生物群落丰度的差异。针对其分析结果,也可以通过可视化绘图,得到相应的物种差异柱状图,或者箱线图等。
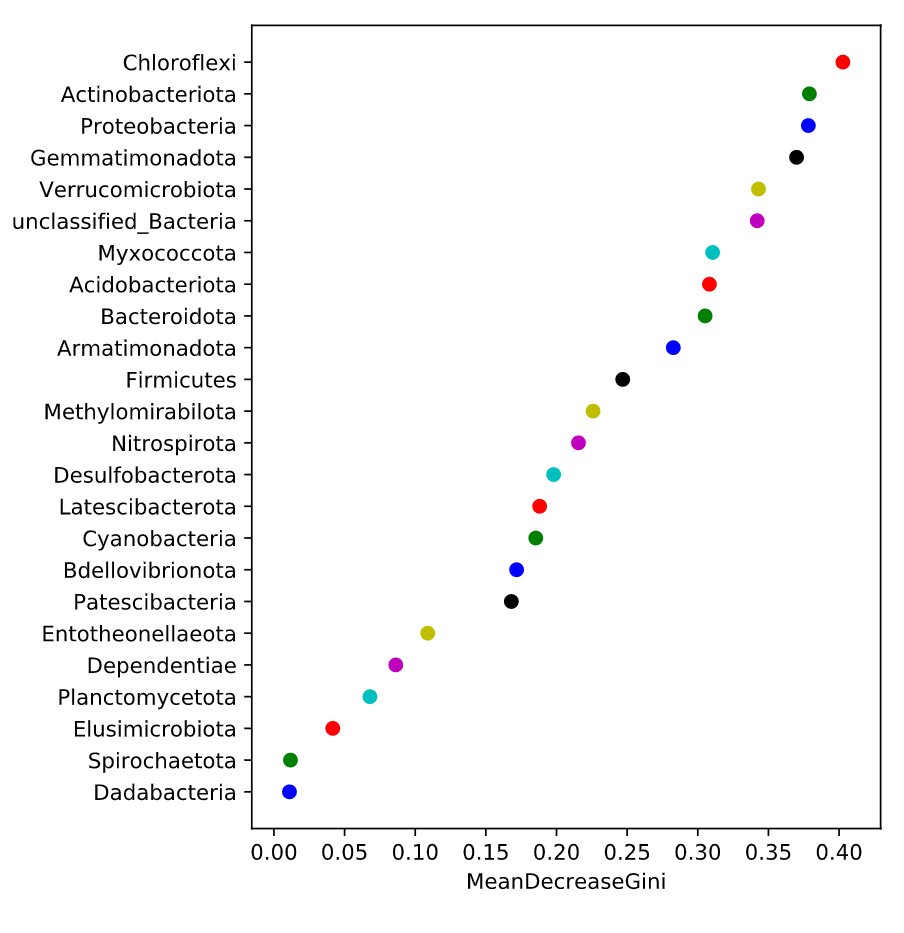
随机森林分析:Random forest 分析,随机森林指的是利用多棵树对样本进行训练并预测的一种分类器,是机器学习的一种。利用随机森林分析可以帮我们找到数据中重要的特征:在微生物组中就是哪些微生物组成可以作为特征进行各种预测;另外,随机森林可以利用这些重要特征构建模型用于分类预测(分类变量)或者回归预测(数值型变量);随机森林分析建议分组内样品至少30个以上,样品数太少影响准确性。 随机森林分析,一般将数据划分为训练数据集(train data)和测试数据集(test or validate data),训练数据集用于构建预测模型,测试集用于查看模型的准确性。
微生物组数据分析方法之:功能基因预测
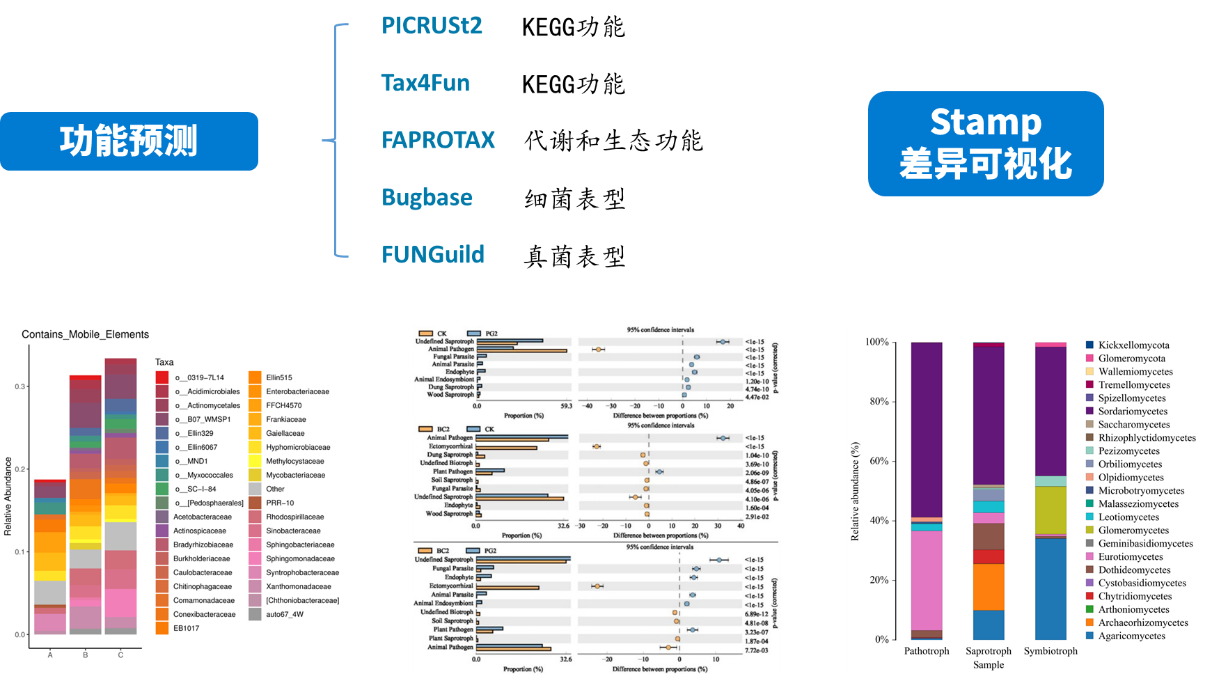
PICRUSt2 (Phylogenetic Investigation of Communities by Reconstruction of Unobserved States)是一款基于样本中的标记基因序列丰度来预测样本功能丰度的软件。这里的功能是指基因家族,如KEGG同源基因、EC酶分类号等,其原理如下图:
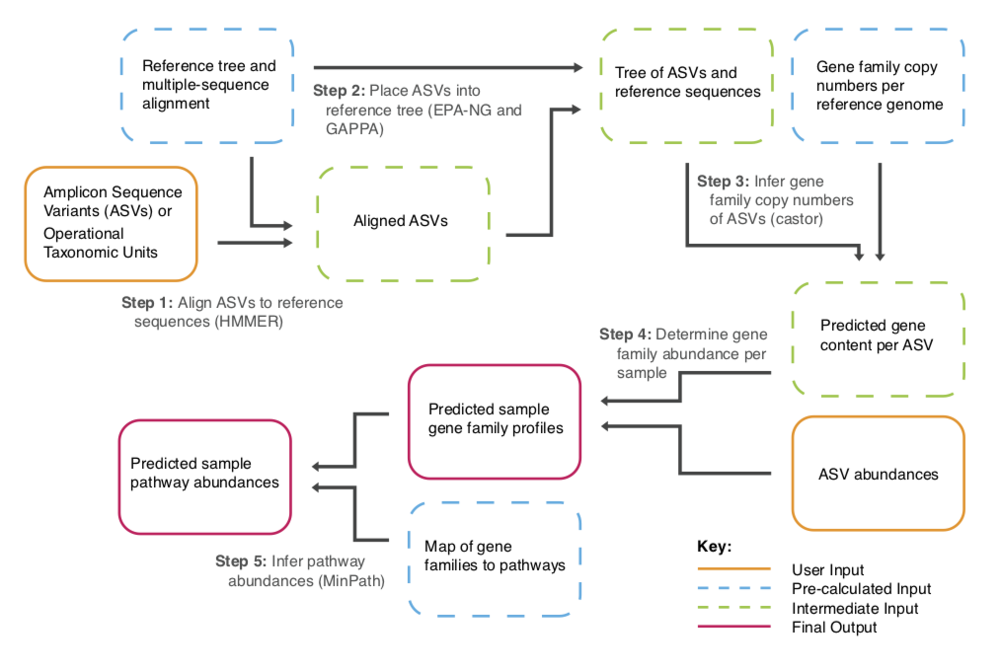
PICRUSt 2 将特征序列(16S rRNA)与微生物基因组数据库(IMG,Integrated Microbial Genomes)参考序列对齐(aliign)构建进化树,找到特征序列的“最近物种”,并根据已知物种的基因种类和丰度信息预测未知物种的基因信息,从而结合基因的KEGG通路信息预测整个群落的通路情况。通过组间差异分析,得到在组间具有显著差异的功能,最后利用Stamp对结果进行差异可视化。
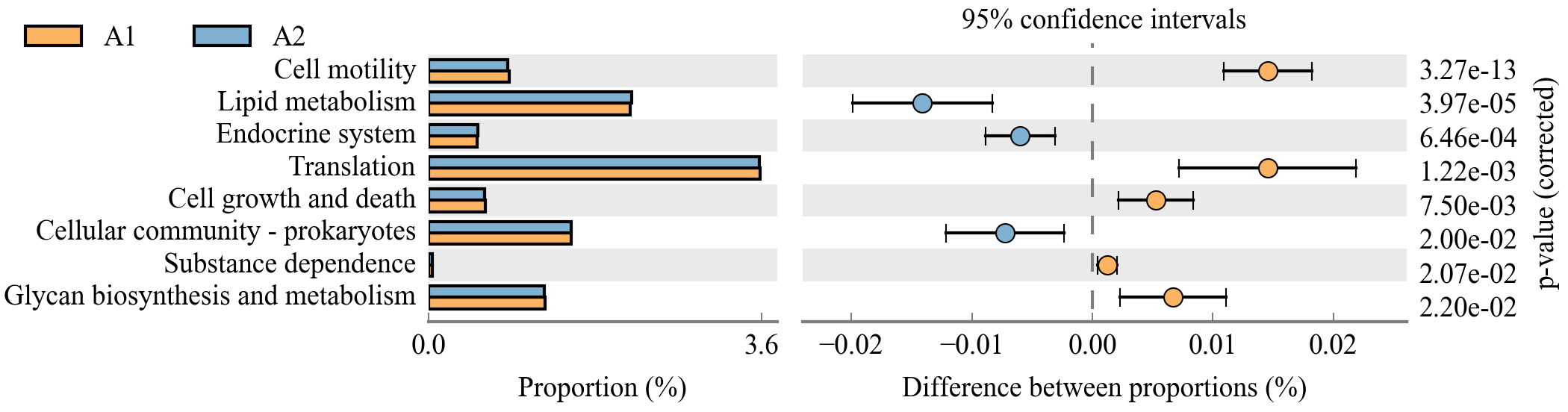 TAX4FUN2: Tax4Fun2可基于16S rRNA基因序列快速预测原核生物的功能谱和功能冗余。通过合并用户定义的、特定于栖息地的基因组信息,可以显著提高预测功能图谱的准确性。不再局限于仅SILVA的特定版本注释的OTU丰度表,允许直接以OTU代表序列作为输入,通过与指定参考数据库的比对实现物种注释。除了Tax4Fun2提供的已构建好的参考集(相比之前大幅扩大),也允许我们提供自定义的参考集,使用非常灵活。
TAX4FUN2: Tax4Fun2可基于16S rRNA基因序列快速预测原核生物的功能谱和功能冗余。通过合并用户定义的、特定于栖息地的基因组信息,可以显著提高预测功能图谱的准确性。不再局限于仅SILVA的特定版本注释的OTU丰度表,允许直接以OTU代表序列作为输入,通过与指定参考数据库的比对实现物种注释。除了Tax4Fun2提供的已构建好的参考集(相比之前大幅扩大),也允许我们提供自定义的参考集,使用非常灵活。
FAPROTAX:较适用于对环境样本(如海洋、湖泊等)的生物地球化学循环过程(特别是碳、氢、氮、磷、硫等元素循环)等生态功能进行预测。FAPROTAX 是根据已发表的文献手动构建的数据库,它把原核微生物的分类和代谢等功能对应起来。因其基于已发表验证的可培养菌文献,其预测准确度较好,但相比于上述PICRUSt2和Tax4Fun来说预测的覆盖度可能会降低。
BugBase:是一种预测复杂微生物组内功能途径的生物水平覆盖以及生物可解释表型的方法。BugBase首先通过预测的16S拷贝数对OTU进行归一化,然后使用提供的预先计算的文件预测微生物表型。包括以下九个方面:Aerobic 好氧、Anaerobic 厌氧、Contains Mobile Elements 移动元件、Facultatively Anaerobic 兼性厌氧、Forms Biofilms ?生物膜形成
Gram Negative 革兰氏阴性、Gram Positive 革兰氏阳性、Potentially Pathogenic 潜在致病性、Stress Tolerant 胁迫耐受。
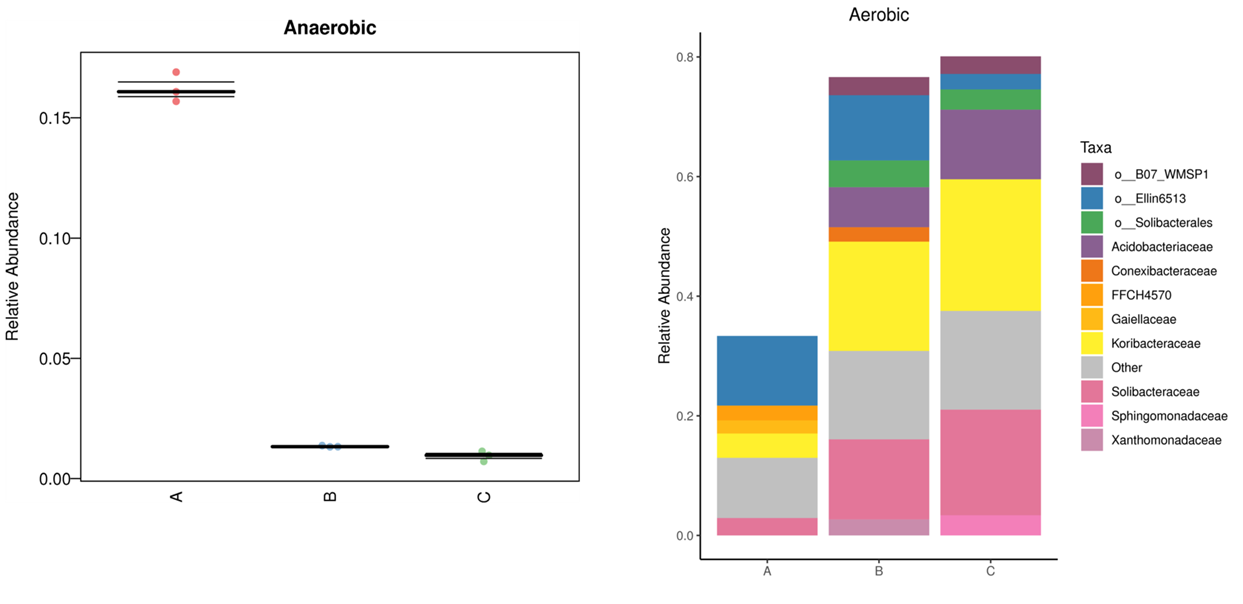
FUNGuild:FUNGuild( Fungi Functional Guild)是一款通过微生态 guild 对真菌群落进行分类分析的工具,guild 是微生态学中的概念,其涉及到一类物种(不管亲缘关系相近与否),这些物种能通过相似的途径利用同类环境资源。
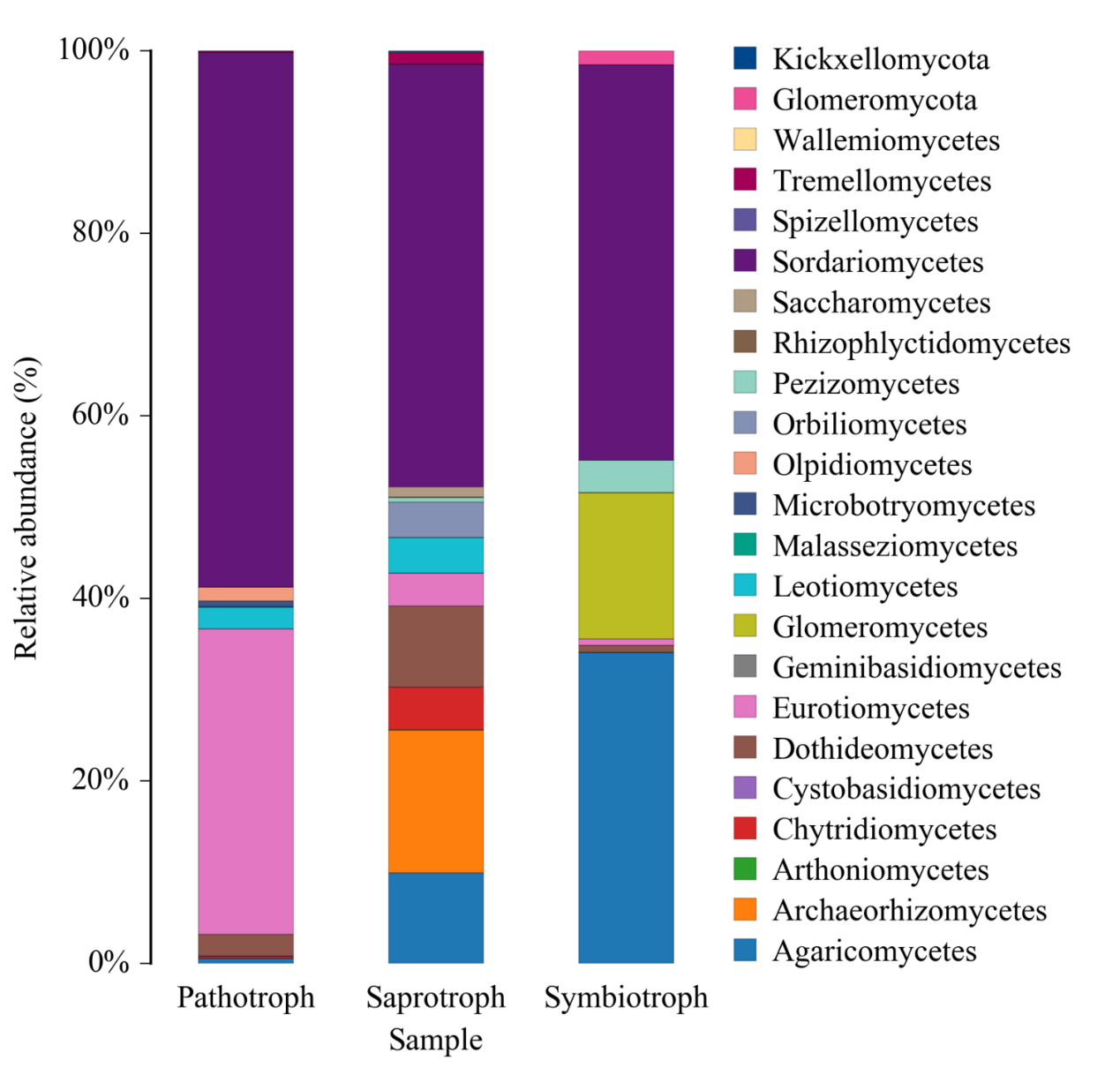
FUNGuild 基于目前已发表的文献或权威网站数据,首先根据营养方式(trophicMode分类系统)将真菌分为三大类:
病理营养型(pathotroph):通过损害宿主细胞而获取营养(包括吞噬型真菌 phagotrophs);
共生营养型(symbiotroph):通过与宿主细胞交换资源来获取营养;
腐生营养型(saprotroph):通过降解死亡的宿主细胞来获取营养。
基于 3 大营养方式,又进一步细分为若干个 guilds,用来对trophicMode 分类系统的补充:
在Pathotroph 下,细分为 Animal Pathogen : 动物病原菌、Plant Pathogen:植物病原菌、Fungal Parasite:真菌寄生菌、Lichen Parasite:地衣寄生菌、Bryophyte Parasite:苔藓植物寄生菌、Clavicipitaceous Endophyte:内生真菌。
在Symbiotroph 下,细分为Ectomycorrhizal:外生菌根、Ericoid Mycorrhizal:杜鹃花类菌根、Lichenized:地衣共生菌等。
在Saprotroph 下,细分成Dung Saprotroph:排泄物腐生菌(如粪便)、Leaf Saprotroph:叶子腐生菌、Plant Saprotroph:植物腐生菌 (生长环境多腐败的植物)、Soil Saprotroph:土壤腐生菌、Wood Saprotroph:木质腐生菌。
基于我们测序得到的真菌序列,就可以进行Guild 的功能注释。
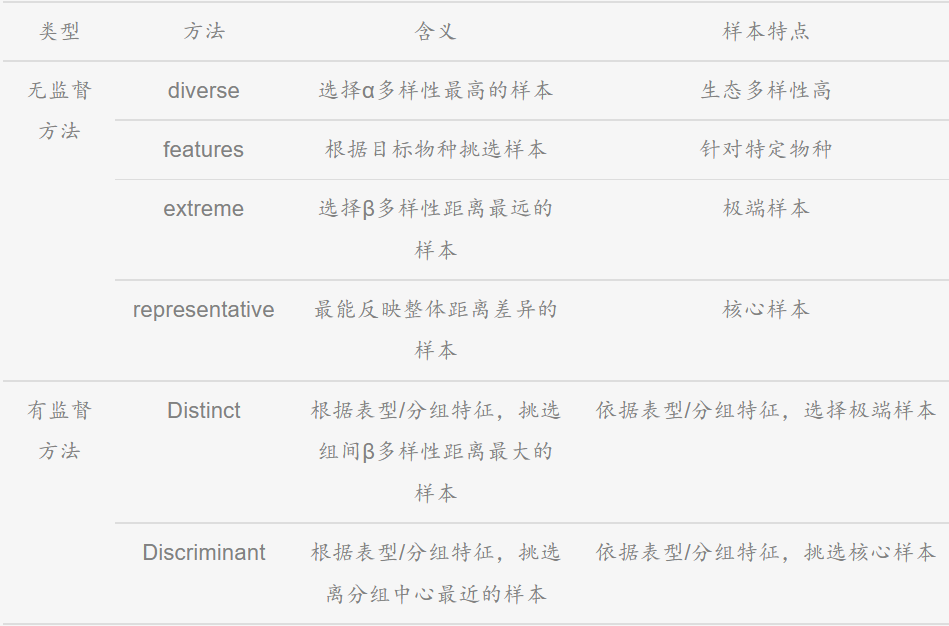
微生物组数据分析方法之:microPITA分析
MicroPITA:在做完16S、18S或ITS等微生物多样性研究后,我们常常还会想进一步了解微生物群落的功能。通常情况下,会采用宏基因组、宏转录组或宏代谢组等方法深入分析,但相对于扩增子测序,宏基因组等测序手段的价格还是相对较高,因此需要从已测完的样本中再挑选合适的样本进行宏基因组测序。可利用microPITA进行样品预测,挑选出合适的样品。该分析是基于大量微生物多样性的数据,根据不同指标筛选出代表性样本,以便于开展开展后续研究。
微生物组数据分析方法之:相关性与关联分析
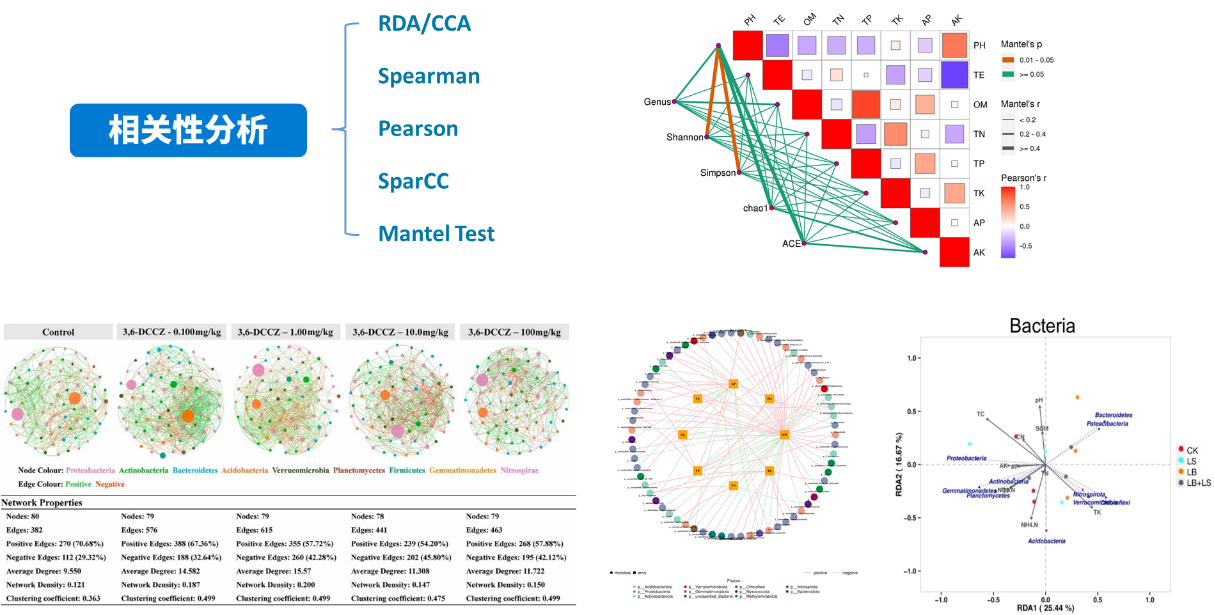
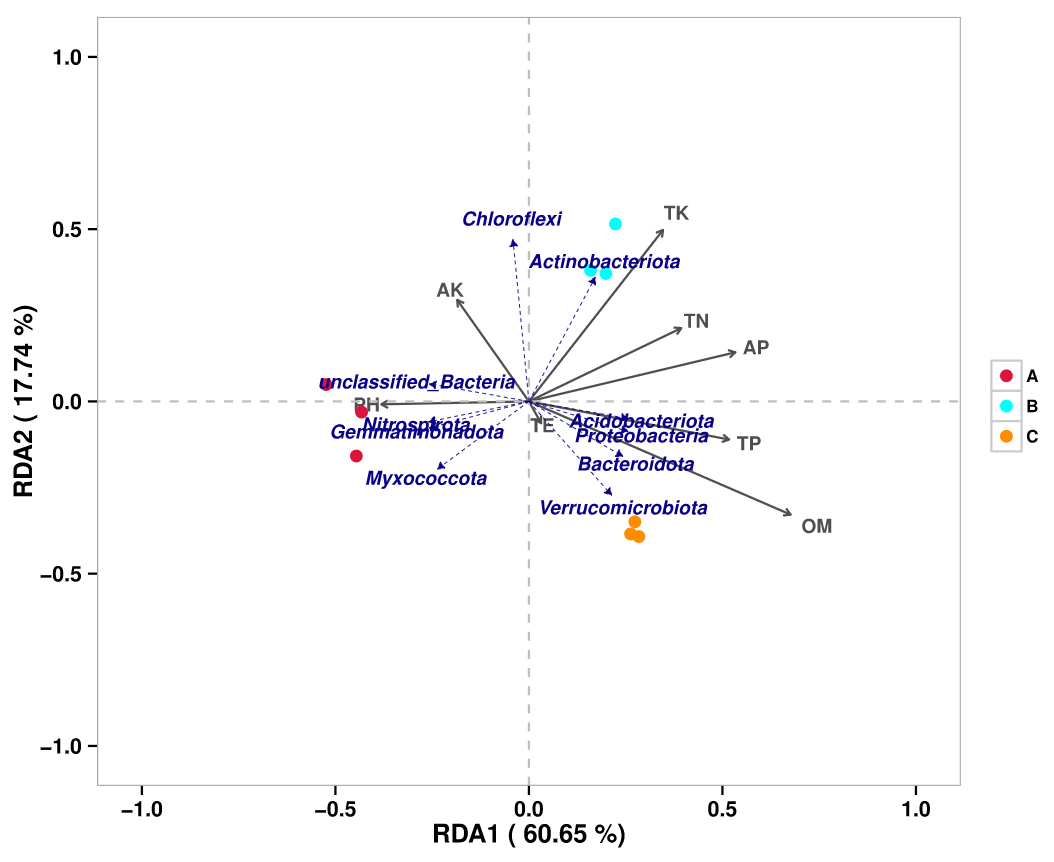
RDA/CCA分析:RDA(Redundancy analysis)/CCA(Canonical Correspondence analysis)是基于对应分析发展的一种排序方法,RDA分析基于线性模型,CCA分析基于单峰模型,主要用来反映菌群或样品与环境因子之间的关系。根据物种分布变化,选择最*的分析模型。
RDA或CCA模型的选择原则:先用species-sample丰度数据做DCA分析,看分析结果中Lengths of gradient 的第一轴的大小,如果大于4.0,就应该选CCA,如果3.0-4.0之间,选RDA和CCA均可,如果小于3.0,RDA的结果要好于CCA。
db-RDA分析:基于距离的冗余分析(db-RDA),db-RDA将主坐标分析(PCoA)计算的样方得分矩阵应用在RDA中,其好处是可以基于任意一种距离测度(例如Bray-curtis距离等,而不再仅仅局限于欧氏距离)进行RDA排序,因此db-RDA在生态学统计分析中被广泛使用。当然,若是我们直接计算样方群落间的欧式距离矩阵并将其输入至db-RDA中计算时,也将会得到和常规的RDA一致的结果。
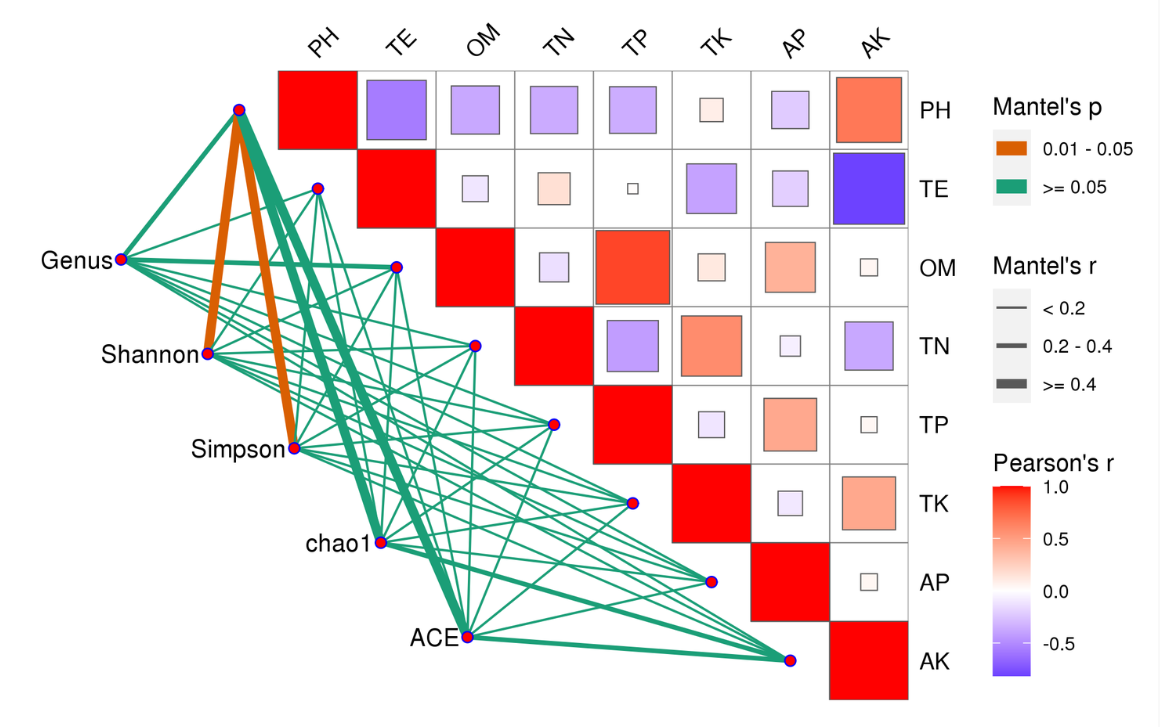
Mantel Test分析:Mantel test 是检验两个矩阵相关关系的非参数统计方法,多用在生态学上,用来检验群落距离矩阵(如 Bray-Curtis distance matrix)和环境变量距离矩阵(即环境因子指标)之间的相关性。其可以得到特征与环境因子之间的mantel test的r值和p值。
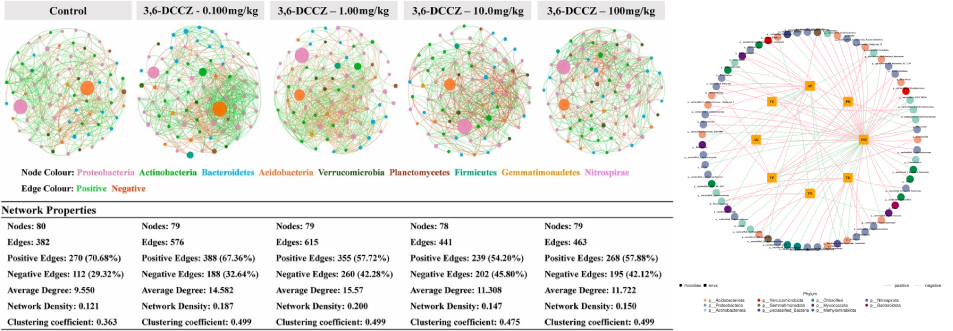
相关性网络分析:网络图是相关性分析的一种表现形式,根据各个物种在各个样品中的丰度以及变化情况,进行斯皮尔曼(Spearman )秩相关分析并筛选相应条件下的数据构建相关性网络。基于网络图的分析,可以获得物种在环境样本中的共存关系,得到物种在同一环境下的相互作用的情况及重要的模式信息,进一步解释样本间表型差异的形成机制。
网络通常由边和节点构成,一条边由两个节点连接而成。网络中节点具有很多重要的性质,包括度、聚类系数、紧密中心性、中介中心性、Zi(within-module connectivity)与 Pi(among-module connectivity)等。通常度、聚类系数、紧密中心性、中介中心性值越大,说明节点重要性越高;此外通过Zi和Pi值可以将节点分为四类:Peripheral nodes(zi?≤?2.5, Pi?≤?0.62,仅有少量的边并且通常只与模块内部的节点相连)、Connectors (zi?≤?2.5, Pi?>?0.62,通常连接不同的模块)、Module hubs (zi?>?2.5, Pi?≤?0.62,与自身所在模块中的许多节点高度连接)和Network hubs (zi?>?2.5, Pi?>?0.62,即能与自身所在模块中的许多节点高度连接又能连接不同的模块),通过这些性质可以说明网络中节点的重要性。
网络自身也具有很多不同的特性,例如节点数据量、边数量、模块性与模块数量、网络直径与密度、平均路径与平均聚类系数等,共同体现网络属性。
VIF(方差膨胀因子)分析:影响菌群的环境因子因素很多,但是有些环境因子间存在较强的多重共线性相关关系,会影响后续分析,因此在环境因子关联分析前,可对环境因子进行筛选,保留共线性较小的环境因子用于后续分析。方差膨胀因子(Variance Inflation Factor,VIF)分析时目前常用的环境因子筛选方法,VIF是衡量多元线性回归模型中复杂(多重)共线性严重程度的一种度量。它表示回归系数估计量的方差与假设自变量间不线性相关时方差相比的比值。其计算公式为:VIFi =1/(1-Ri^2),其中Ri^2代表模型中与其它自变量相关的第i个自变量的方差比例,用于衡量第i个自变量与其它自变量间的共线性关系。VIF越大,显示共线性越严重。经验判断方法表明:当VIF大于0且小于10,不存在多重共线性;当VIF大约等于10且小于100,存在较强的多重共线性;当VIF大于等于100,存在严重多重共线性,因此通常认为小于10的环境因子是无用的环境因子。
VPA分析(方差分解分析):VPA,全称Variance Partitioning Analysis,中文称为方差分解分析,该分析的目的是确定指定的环境因子对群落结构变化的解释比例。通常在CCA/RDA的排序分析方法可以得到所有参与分析的环境因子对群落变化的解释比例。使用R语言vegan包(version:2.3-0),varpart函数进行分析;分析前首先需要对环境因子进行一个分类,一般支持2-4类,默认使用大于等于2个环境因子进行此分析。
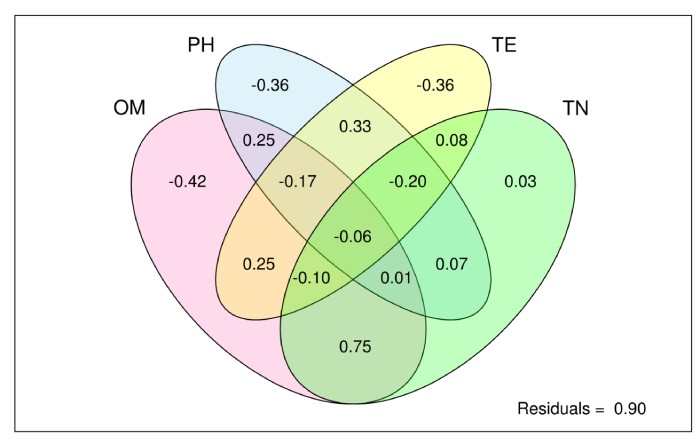
微生物组数据分析方法之:溯源分析
SourceTracker 分析:SourceTracker—微生物来源分析,用途是可以识别相关各组间来源的分析,如婴儿的肠道菌群有哪些继承了母亲的肠道菌群、哪些来自阴道菌群、哪些来自皮肤;河流污染物的来源分析、周围工厂、农田、养殖厂对河流污染的贡献和来源追溯等。可以估计末知群体微生物来源和组成,有用的是可根据环境样品来分类微生物的来源。
目标样本为Sink,微生物污染源或来源的样品为Source;基于贝叶斯算法,探究目标样本(Sink)中微生物污染源或来源(Source)的分析。根据Source样本和Sink样本的群落结构分布,来预测Sink样本中来源于各Source样本的组成比例。
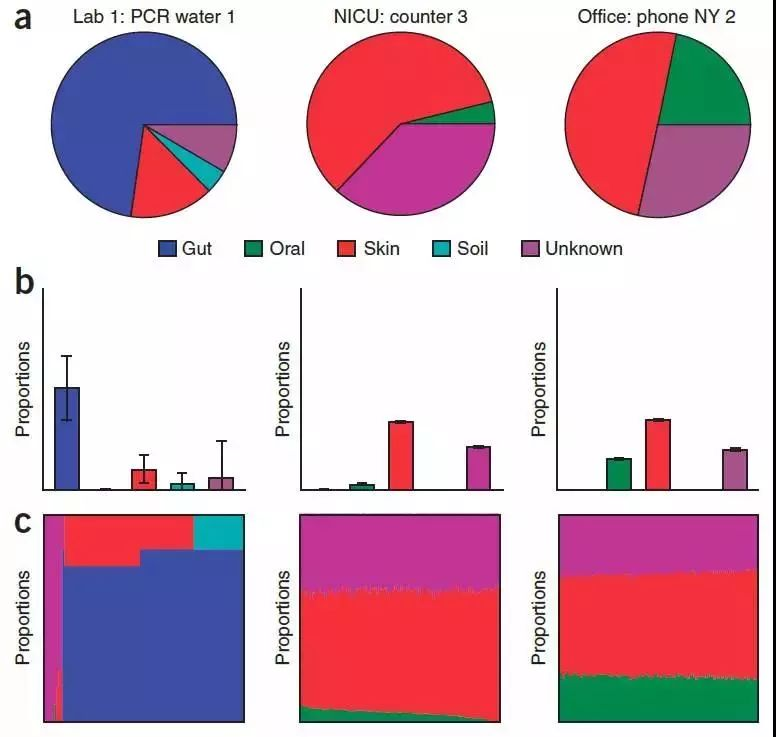
SourceTracker对水槽样本子集的比例估计
参考文献:Knights D, Kuczynski J, Charlson ES, et al. Bayesian community-wide culture-independent microbial source tracking [J]. Nature Methods, 2011, 8(9): 761.
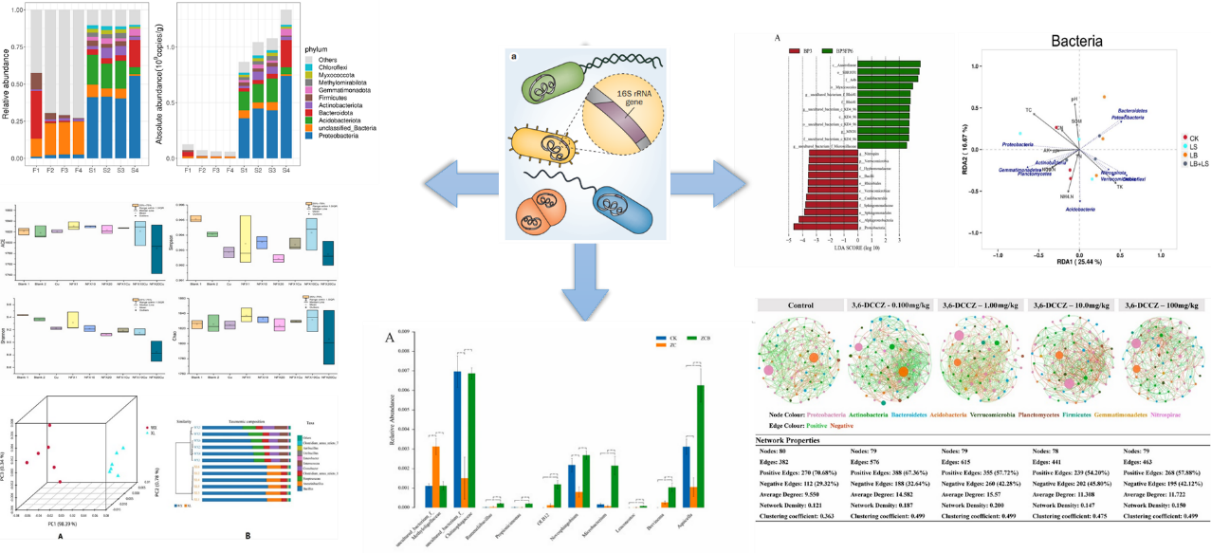
文章中部分图表展示
如果您对以上分析方案感兴趣,欢迎点击下方按钮联系我们,我们将免费为您设计文章思路方案
参考文献:
[1] Liu A, Wang W, Chen X, et al. Rice-associated with Bacillus sp. DRL1 enhanced remediation of DEHP-contaminated soil and reduced the risk of secondary pollution through promotion of plant growth, degradation of DEHP in soil and modulation of rhizosphere bacterial community[J]. Journal of Hazardous Materials, 2022, 440: 129822.
[2] Chen X, Chen J, Yu X, et al. Effects of norfloXacin, copper, and their interactions on microbial communities in estuarine sediment[J]. Environmental Research, 2022: 113506.
[3] Wang C, Hu R, Strong P J, et al. Prevalence of antibiotic resistance genes and bacterial pathogens along the soil–mangrove root continuum[J]. Journal of Hazardous Materials, 2021, 408: 124985.
[4] Zhang W, Gong W, Zhang Z, et al. Bacterial communities in home-made Doushen with and without chili pepper[J]. Food Research International, 2022, 156: 111321.
[5] Whiteside S A, Razvi H, Dave S, et al. The microbiome of the urinary tract—a role beyond infection[J]. Nature Reviews Urology, 2015, 12(2): 81-90.
[6] Liu Y X, Qin Y, Chen T, et al. A practical guide to amplicon and metagenomic analysis of microbiome data[J]. Protein & cell, 2021, 12(5): 315-330.









 京公网安备 11011302003368号
京公网安备 11011302003368号